Learning Algorithms for Robotic application

1 - Introduction

Generally we are used to see articles or demos on deep/machine learning methods just on video applications. In this article we want review and apply the current AI into future trends for robotics, such as learning algorithm.

Let say that there is not a general definition for AI, but the one we selected is that a system is “intelligent” if it achieves a specific goal in a generic situation.

We can define a robotic system as a complex system composed of many heterogeneous components, generally we would have cameras for the perception part, the mechanics which physically compose the robots and electronics which is usually the controller of the whole system.

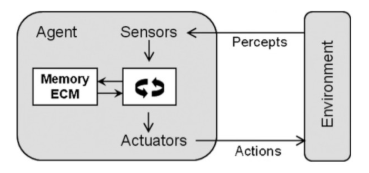
Schematic of a robotic system for learning algorithm — Figure 1: Schematic of a robotic system.

Now that we have clear in mind a general idea of a robotic system and a possible definition of intelligent system, let’s discuss a little bit on what application can we have.

The most common applications are the industrial robots and automotive ones, like a robotic arm that must perform a “pick and place” task or an autonomous car.

The first example is a very common study example, but very interesting because it can be applied in many different situations and can be used to test different events (i.e. collision avoidance).

The second example is perfect to enlighten the previous picture, because autonomous cars can for example perceive the environment using LIDAR and cameras, out of which extracting the information of what is present in the scene and reconstruct their positions in space. The information is used for example for trajectory planning.

Let’s dig a little bit on the strategies that can be taken into account to make a robot autonomous with learning algorithms.

2 - Some Learning algorithms

We consider three main methods:

Supervised Learning: This choice implies that we have full control of the training and testing dataset, and so we can deduce the results of the learning session.
Unsupervised Learning: This choice implies that we have no control on the testing dataset or even we have no training dataset.
Reinforcement learning: The basic idea behind this method is that the robot can learn by its experience, in order to avoid replicating the errors previously committed.

In robotics, the various communities have different approaches to the problem of making a robot autonomous or semi-autonomous and reinforcement learning is our target with the cart-pole system example. In this situation we have a cart that has keep a stick in vertical equilibrium.

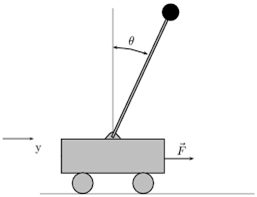
Cart pole system — Figure 2: Cart-Pole system

Although we have an analytical solution of this system, it is often used to introduce reinforcement learning.

In reinforcement learning we need two main structure:

Goal State: This structure is used to define what we expect from the robot to reach at the end of a sequence of actions.
Policy: This structure is used to define a function which returns a reward based on the pair action-state and previous action-state. The reward is used to understand the best way to reach the goal state.

In this case, the goal state could be the state used to represent the stick which has a value (corresponding to the vertical position), and the policy could be a set of forces applied to the car (actions) in order to reach and maintain this state.

There are two famous algorithms for reinforcement learning:

Q-Learning
State–Action–Reward–State–Action (SARSA)

I will not introduce them, but the reader can find its definition in the link above. We apply instead Artificial Neural Network for solving the problem.

We have already written an article on that topic applied to FPGA, if the reader would like to read it, this is the link:

https://www.makarenalabs.com/ai-edge-platform-on-zynq-fpga/

So, how can we adapt reinforcement learning to deep reinforcement learning?

The choice made by many engineers is to create two networks, one for the actual learning/performing task, and one which gives the reward as a feedback for a certain evaluation of the pairs action-state.

The most famous example is probably the network of DeepMind (https://deepmind.com/), which succeeded to overcome the world champion of GO, by using deep reinforcement learning as the technique to learn how to play better. The idea behind, is that the network can play many games and understand via the reward network if it is playing correctly or it needs to change to reach the goal state.

As the end of this chapter I want to introduce briefly a new learning approach, which will be explained in the next chapter with a practical example.

The new approach is called Learning from demonstration. The title is self-explanatory, and it consists of a robot learning from a human which executes one or more tasks. We now focus on a framework which uses this technique.

3 - Dynamic Movement Primitives for learning algorithms

Before starting, let me underline something very important. Math and Physics are really what every scientist or engineer needs while working with actual problems, i.e. analysis or algebra is not something just related to a university exam, but to the construction of our way of describing the world.

The focus of this chapter will be just a brief introduction of the framework just for autonomous trajectory execution.

Let’s think a little bit of what we need to execute a trajectory autonomously from a robot. We want this execution to be easily learned and invariant under affine transformations, that is a geometric transformation that preserves lines and parallelism (but not necessarily distances and angles), such that for example a simple translation will not break everything up. We also want that the trajectory learned is robust for collision avoidance, or rather if exists a simple way to make the robot divert its trajectory without performing again a learning session.

There exists a framework which is robust to all the previous points and it is called Dynamic Movement Primitives.

This framework is so described:

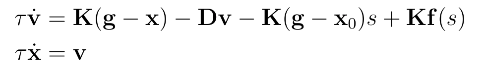
DMP formulation for learning algorithm — Figure 3: DMP formulation

The DMP is a dynamical system composed of two first order differential equations (ODE). K and D terms are respectively a spring and a damper, whereas x and v stands for position and velocity. We have a non-linear forcing term f(s) also called perturbation which encodes the shape of trajectory, and is the actual term where the learning part is performed. Finally g represents our goal and xo our start position.

I do not want to dig much on that, but just look that the system is stable in the point (x,v) = (g, 0), notice that is actually the goal.

The system is also invariant under affine transformations.

The geometric meaning of the DMP is that the states of the system are attracted by a spring-damper system in a “hole” (which geometrically represent the fact that system is stable) into which the goal lies, and the landscape where the states lies is modelled by the non-linear forcing term, so the learning part consists in the modification of such landscape in order to perform the correct trajectory.

What is missing is the collision avoidance, but how to compute it? We need two structures:

Something which describes how to perform a steering angle, and another to describe the obstacle.
A camera or anything else which can give us the feedback information on the shape of the obstacle.

Having those other structures, we can introduce a new term in the equation, called repulsive. This term is used to “push” away the robot from its original trajectory to perform collision avoidance. So the first equation becomes:

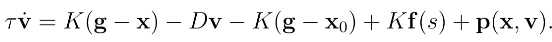
DMP re-formulation considering collision avoidance for learning algorithm — Figure 4: DMP re-formulation considering collision avoidance

The term p(x,v) is the repulsive term, and it can be formulated in various ways, depending on our choices. This term allows us to perform the obstacle avoidance in real time, because it is just a function that can easily compute once defined.

Last consideration on DMP, but not least, is the fact that the robot can learn the execution by just one demonstration, because after the computation of the forcing term and the parametrization of the trajectory, you just need to set the spring-damper system and begin the execution.

4 - Appendix and conclusions

We are at the end of our brief discussion on learning approaches for robotics. We have focused on two of them especially, reinforcement learning and learning from demonstration. We have also introduced a framework for the last discussed approach.

Nowadays there is a great interest between the study of Deep Reinforcement Learning, because instead of having a “classical” dataset out of which executing the learning algorithms, the robot learns how to perform certain tasks by its experience. This type of learning very well fit situations in which the robot has to perform sequential decisions for a long term goal. This type of learning could be easily for example adapted for a “pick and place” task in industry, by diving the action in many steps and performing the Deep Reinformcement Learning with rewards for every single step chosen.

For what concern the Learning from Demonstration, there is a lot of interest in the community, because it allows to perform very complex movement or tasks learned with little effort and great precision. This is possible due the fact that the single task learned can be easily concatenated to other.

Let me state again that this was just a brief introduction, so the reader is encouraged to elaborate on the references and also on other sources they will find on the net or in books.

Thanks for reading and enjoy your acceleration